
9、微分中值定理,泰勒公式
费马定理

罗尔定理

拉格朗日中值定理

柯西中值定理

10、洛必达法则
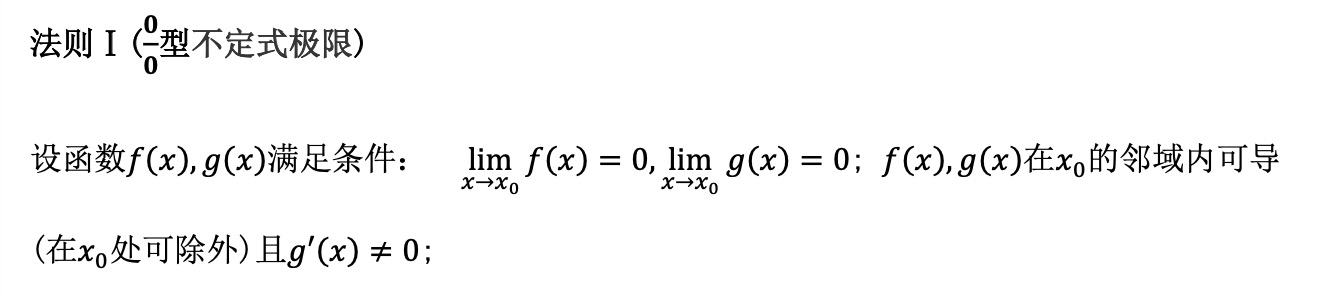

11、泰勒公式

常用五种函数在0 = 0处的泰勒公式 :

12、函数单调性的判断
设函数()在(, )区间内可导,如果对∀ ∈ (, ),都有 ′() > 0(或 ′() < 0),则函数()在(, )内是单调增加的(或单调减少)。
(取极值的必要条件)设函数()在0处可导,且在0处取极值,则 ′(0) = 0。
(取极值的第一充分条件)设函数()在0的某一邻域内可微,且 ′(0) = 0(或()在0处连续,但 ′(0)不存在)。若当经过0时, ′()由“+”变“-”,则(0)为极大值;若当经过0时, ′()由“-”变“+”,则(0)为极小值;若 ′()经过 = 0的两侧不变号,则(0)不是极值。
(取极值的第二充分条件)设()在点0处有′′() ≠ 0,且 ′(0) = 0,则:
当′ ′(0) < 0时,(0)为极大值; 当′ ′(0) > 0时,(0)为极小值. 注:如果 ′ ′(0)0,此方法失效。
13、渐近线的求法

14、函数凹凸性的判断
(凹凸性的判别定理)若在 I 上′′() < 0(或′′() > 0), 则()在 I 上是凸的 (或凹的)。(拐点的判别定理 1)若在0处′′() = 0,(或′′()不存在),当变动经过0时, ′′()变号,则(0, (0))为拐点。(拐点的判别定理 2)设()在0点的某邻域内有三阶导数,且′′() = 0,′′′() ≠ 0,则(0, (0))为拐点。
15、弧微分
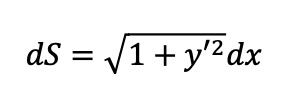
16、曲率

17、曲率半径

版权声明:我们致力于保护作者版权,注重分享,被刊用文章【证明函数在区间内可导(机器学习之高等数学总结下)】因无法核实真实出处,未能及时与作者取得联系,或有版权异议的,请联系管理员,我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理!;
原文链接:https://www.yxiso.com/zhishi/2132702.html

